It is a well known fact that careful curation and tweaking of your real-valued input data is of great importance to successful learning using stochastic gradient descent and the likes.

From Deep learning with Python : a hands-on introduction p. 131:

Preprocessing Input Data
It is of utmost importance that data is scaled well so as to ease the optimization ... A good rule of thumb is to standardize the data by subtracting the mean and divide by the standard deviation to scale the data.

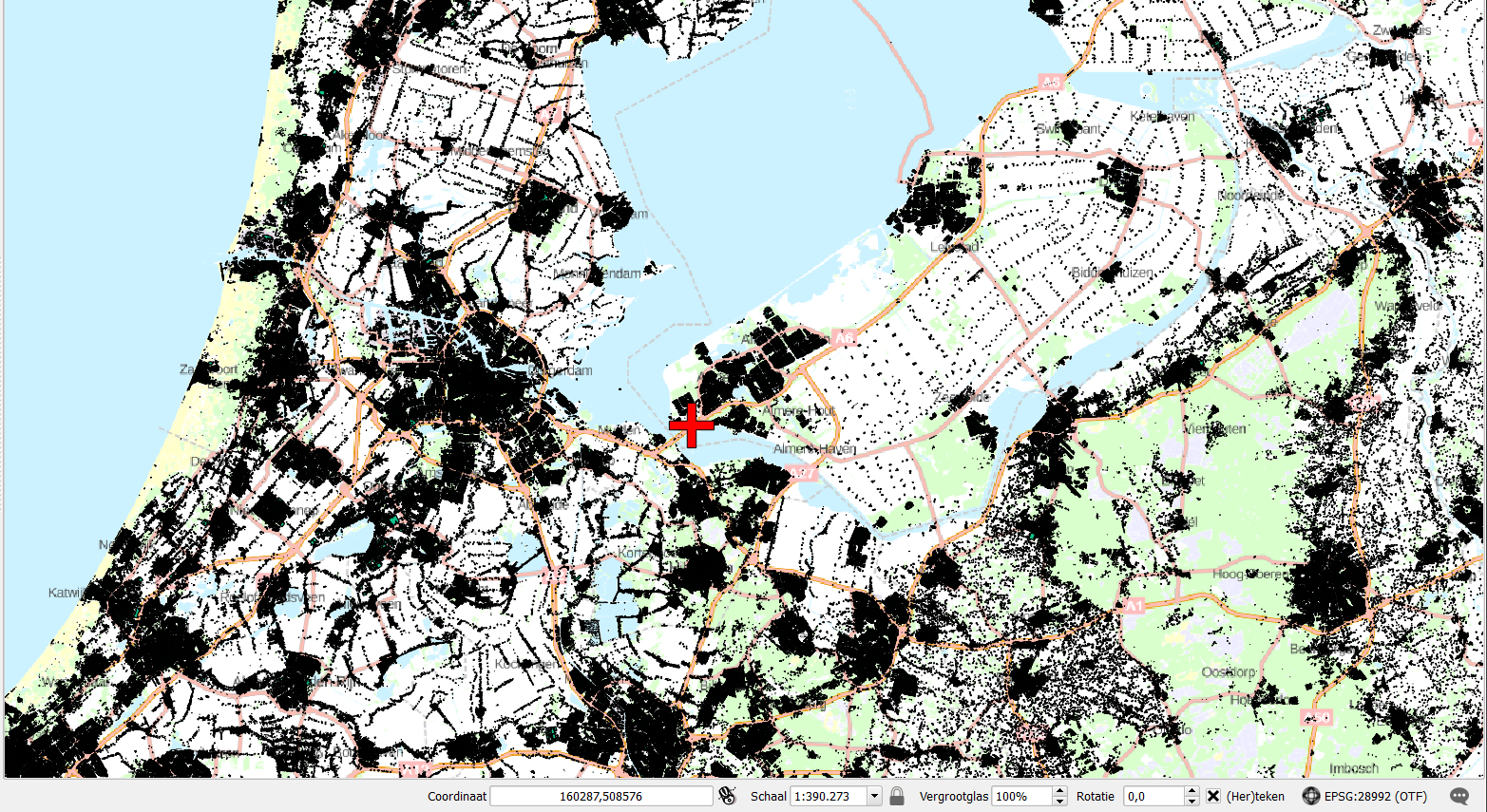
The problem with local processing of wide-scale data is that the mean is somewhere in the middle of the data, spanning a potentially huge area. x marks the mean spot

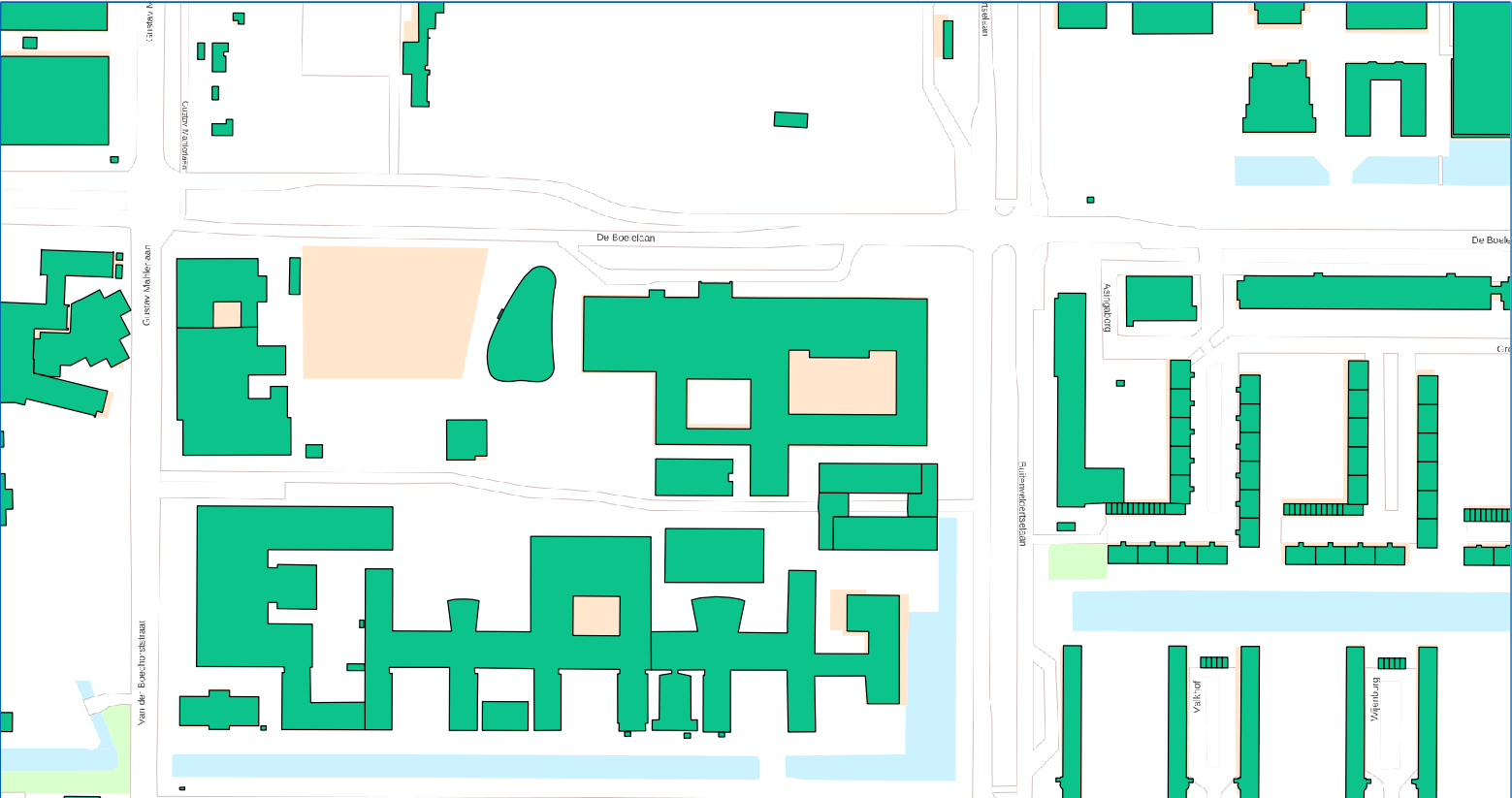
So, while the learning task operates on a decimeter level, the data set itself spans hundreds of kilometers, a scaling problem of a factor of 1.000.000. This is the scale on which I do te learning task: local topology

Standard data normalization methods that operate on the data set as a whole can’t bring down the problem because of the spread of the data: the mean is somewhere in the center of the data of the entire country, the variance is huge.

Batch normalization won’t help you here, because of the spatial spread of the data. Standard scikit-learn preprocessing methods won’t work because of the same reason.

Solution

The input data needs to be shifted and scaled to a custom location for every single data point to be in the range of the target. This means creating a localized (0, 0) origin for every record. At the moment I do this by

base_precision = 1e6
base = np.floor(base_precision * training_vectors[:, 0:1, :])
base = np.repeat(base, 2, axis=1)
training_vectors = (base_precision * training_vectors) - base

but this is untenable because now I can’t reconstruct the original location of the data point, which is a problem as soon as I want to learn intersection geometries. It’s not a critical problem, but it would be a lot nicer if the network could produce the output geometries end-to-end, without the need for post-processing. Post-processing is an option, because once trained, you could imagine an API that uses a set of two input geometries, normalizes to a localized mean and sigma, makes the model predict the intersection and invert the localized normalization on the output.

So, should I require the network to (soft) learn the transformation parameters for this localized origin or should it be (hard) inserted through logic? If it is to be inserted through logic, how can this be achieved? Maybe I’m going to have to implement a custom layer with tied weights and bias…

Solution

Further reading